This article discusses cubic equations in one variable. For a discussion of cubic equations in two variables, see elliptic curve.
In mathematics, a cubic equation is a polynomial equation of the third degree. The general form of a cubic equation is

where

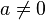
(if a = 0, then the equation becomes a quadratic equation).
Usually, the coefficients a, b, c, d are real numbers. However, most of the theory is also valid if they belong to a field of characteristic other than two or three. We will always assume that a is non-zero (otherwise it is a quadratic equation).
Solving a cubic equation amounts to finding the roots of a cubic function.

History
Every cubic equation with real coefficients has at least one solution x among the real numbers; this is a consequence of the intermediate value theorem. We can distinguish several possible cases using the discriminant,

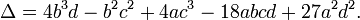
The following cases need to be considered.
See also: multiplicity of a root of a polynomial

If Δ < 0, then the equation has three distinct real roots.
If Δ > 0, then the equation has one real root and a pair of complex conjugate roots.
If Δ = 0, then (at least) two roots coincide. It may be that the equation has a double real root and another distinct single real root; alternatively, all three roots coincide yielding a triple real root. A possible way to decide between these subcases is to compute the resultant of the cubic and its second derivative: a triple root exists if and only if this resultant vanishes. The nature of the roots
The solutions can be found with the following method due to Scipione del Ferro and Tartaglia, published by Gerolamo Cardano in 1545.
We first divide the standard equation by the leading coefficient to arrive at an equation of the form

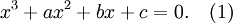
The substitution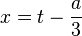 eliminates the quadratic term; in fact, we get the equation

This is called the depressed cubic.
Suppose that we can find numbers u and v such that

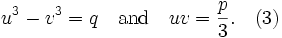
A solution to our equation is then given by

as can be checked by directly substituting this value for t in (2), as a consequence of the third order binomial identity

The system (3) can be solved by solving the second equation for v, which gives

Substituting this into the first equation in (3) yields

Moving the q to the other side and multiplying by 27u. If we solve this equation, we find that

Since t = v − u, t = x + a/3, and v = p/3u, we find

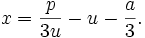
Note that there are six possibilities in computing u with (4), since there are two solutions to the square root (), and three complex solutions to the cubic root — the principal root and the principal root multiplied by . However, the sign of the square root (plus or minus) does not affect the final resulting x, although care must be taken in two special cases to avoid divisions by zero. First, if p = 0, then one should choose the positive square root so that u does not equal zero, i.e., 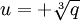p = q = 0, then we have the triple real root x = −a/3.
In summary, for the cubic equation

the solutions for x are given by

where



Cardano's method
The symmetric group S₃ has the cyclic group of order three as a normal subgroup, which suggests making use of the discrete Fourier transform of the roots, an idea due to Lagrange. Suppose that r₀, r₁ and r₂ are the roots of equation (1), and define , so that ζ is a primitive third root of unity. We now set



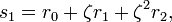
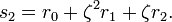
The roots may then be recovered from the three s_i by inverting the above linear transformation, giving



We already know the value s₀ = −a, so we only need to seek values for the other two. However, if we take the cubes, a cyclic permutation leaves the cubes invariant, and a transposition of two roots exchanges s₁, hence the polynomial

is invariant under permutations of the roots, and so has coefficients expressible in terms of (1). Using calculations involving symmetric functions or alternatively field extensions, we can calculate (5) to be

The roots of this quadratic equation are

where Δ is the discriminant defined above. Taking cube roots give us s₁ and s₂, from which we can recover the roots r_i of (1).

Factorization
The formula for finding the roots of a cubic function is fairly complicated. Therefore, it is common for some students to use the rational root test or a numerical solution instead.
If we have

let

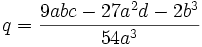
and

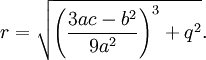
Now, let
and
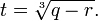The solutions are




Solution in terms of a, b, c, and d
If we have a cubic equation which is already in depressed form, we may write it as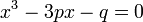 . Substituting we obtain 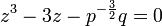or equivalently

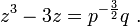
From this we obtain solutions to our original equation in terms of the Chebyshev cube root as



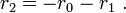
If now we start from a general equation

and reduce it to the depressed form under the substitution x = t − a/3, we have and 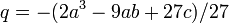, leading to

This gives us the solutions to (1) as




Solution in terms of Chebyshev radicals
Suppose the coefficients of (1) are real. If s is the quantity q/r from the section on real roots, then s = t + 3x − t with real t, this is a convenient way to solve for its roots.

See also
"The Egyptians considered the solution impossible, but the Greeks came nearer to a solution."
"Khayyam himself seems to have been the first to conceive a general theory of cubic equations."
"Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics."